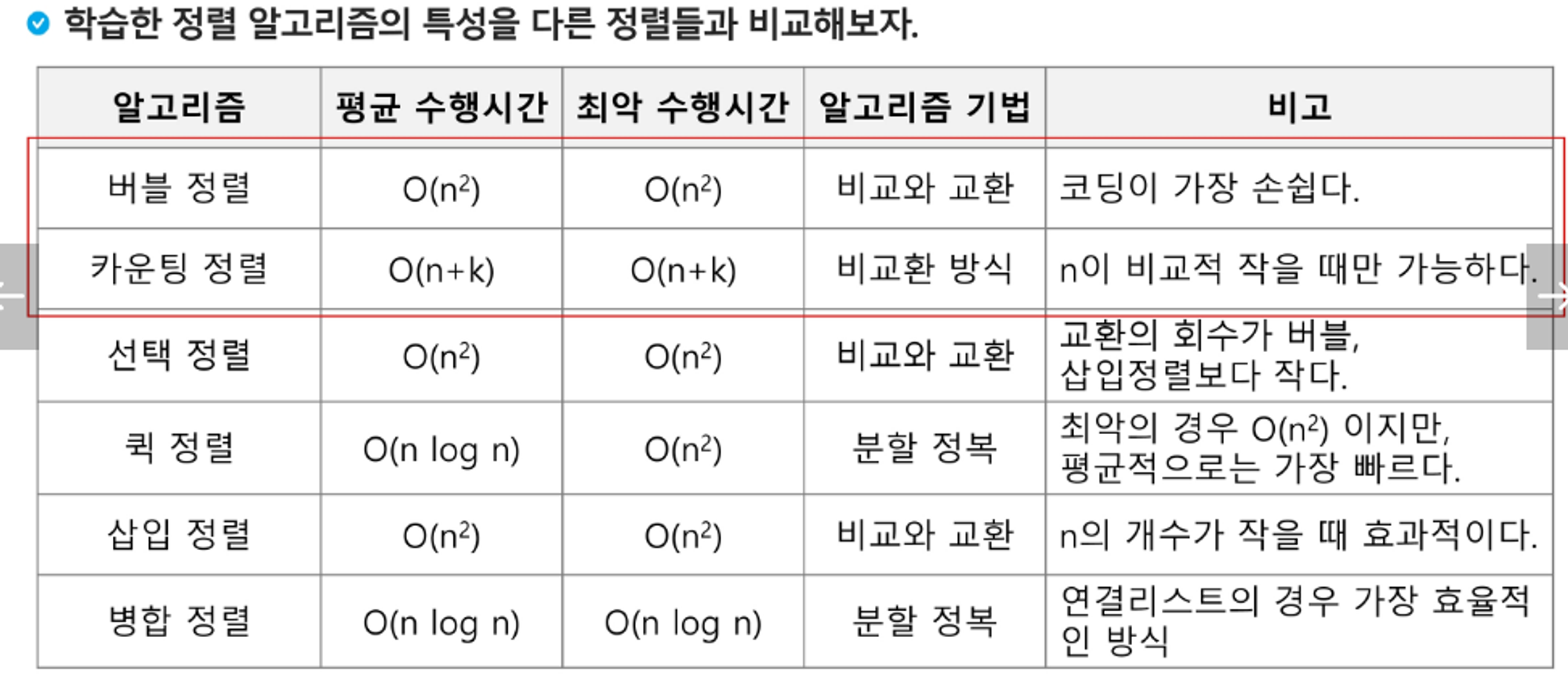
버블 정렬
인접한 두 개의 원소를 비교하며 자리를 계속 교환하는 방식 (비교, 교환)
파괴형이다 : 원본 리스트를 직접 바꿔버리기 때문
과정
- 첫번째 원소부터 인접한 원소끼리 계속 자리를 교환하면서 맨 마지막자리까지 이동한다.
- 한 단계가 끝나면 가장 큰 원소가 마지막 자리로 정렬된다.
구간의 갯수가 n개면 0번 인덱스부터 n-1번 인덱스까지 한다.
…
구간의 갯수가 2개면 0번 인덱스부터 1번 인덱스까지 한다
n개의 데이터를 버블 정렬로 정렬 하기 위해서는 n-2번쨰 인덱스까지 봐야되구나
⇒ n-1번째 인덱스를 i로 시작해서 1번째 인덱스까지 뒤에서 부터 결정한다
⇒ 왜냐? 버블소트의 가장 첫 시행 때 가장 큰 수가 가장 마지막에 정렬된다.
for i:N-1 -> 1 #정렬될 구간의 끝
for j:0 -> i-1 # 비교할 원소 중 왼쪽 원소의 인덱스 # N-2 가 아닌 이유 : 뒤에서 부터 정렬이 완료되기 때문에, # 정렬을 해야되는 갯수가 줄어들기 때문
if A[j] > A[j +i] # 왼쪽 원소가 더 크면 A[j] <-> A[j + 1] #오른쪽 원소와 교환
#파이썬 코드
for i in range(N-1,0,-1): #범위의 끝 위치
for j in range(0,i): #비교할 왼쪽 원소
if a[j] > a[j+1]: a[j], a[j+1] = a[j+1], a[j]배열을 활용한 버블 정렬
N = 6
arr = [7, 2, 5, 3, 1, 5]
def asc(arr, N): #오름차순 # for i : N-1 -> 1, 정렬할 구간의 마지막 인덱스 for i in range(N-1,0,-1): # for j : 0 -> i-1 , j는 비교할 두 원소 중 왼쪽의 인덱스 for j in range(i): if arr[j] > arr[j+1]: # 오름차순은 큰 수를 오른쪽으로 arr[j], arr[j+1] = arr[j+1],arr[j]
def dec(arr, N): #내림차순 # for i : N-1 -> 1, 정렬할 구간의 마지막 인덱스 for i in range(N - 1, 0, -1): # for j : 0 -> i-1 , j는 비교할 두 원소 중 왼쪽의 인덱스 for j in range(i): if arr[j] < arr[j + 1]: # 내림차순은 작은 수를 오른쪽으로 arr[j], arr[j + 1] = arr[j + 1], arr[j]
asc(arr, N)
print(arr)
dec(arr, N)
print(arr)카운팅 정렬
항목들의 순서를 결정하기 위해 집합에 각 항목이 몇 개씩 있는지 세는 작업을 하여, 선형 시간에 정렬하는 효율적인 알고리즘
비 파괴형이다. : 새로운 리스트로 만들기 때문
제한 사항
카운트들을 위한 충분한 공간을 할당하려면 집합 내의 가장 큰 정수를 알아야 함
정수 or 정수로 표현할 수 있는 자료(소수점 2자리로 된 실수, 아스키 코드로 바꾼 문자 등) 에 대해서만 적용 가능 : 각 항목의 발생 회수를 기록하기 위해, 정수 항목으로 인덱스 되는 카운트들의 배열을 사용하기 때문
시간 복잡도
n 은 리스트 길이, k는 정수의 최대 값
Data에서 카운트를 만들 때 n번
카운트를 훑을 때 k 번
Temp를 만들어서 뒤에서 부터 하나씩 비교할 때 n번
과정
[0, 4, 1, 3, 1, 2, 4, 1]
- 1-1 단계, 개수 세기
Data에서 각 항목들의 발생 회수를 세고, 정수 항목들로 직접 인덱스 되는 카운트 배열 counts에 저장한다.
#데이터가 들어갈 칸, 많으면 상관없으면, 모자르면 indexError
counts = [0] * (K+1)
for x in DATA #데이터에 있는 애들을 모두 꺼내서
counts[x] += 1 # 해당 위치의 카운트를 하나씩 올리겠다 #counts[0] ++ #슈도코드- 1-2 단계, 개수 누적시키기 stable sort(안정정렬)
정렬된 집합에서 각 항목의 앞에 위치할 항목의 개수를 반영하기 위해 counts의 원소를 조정한다.
counts 1 3 1 1 2 (index 당 counts 개수)
⇒ counts 1 4 5 6 8 (index 당 counts 누적 개수)
0번째 인덱스는 항상 전 후가 같다
for i : 1 → k
counts[i] <- counts[i-1] + counts[i]
#누적된 개수를 추가할 수 있다.
for i in range(1,k+1): # 왜 1부터인가? i-1 을 사용해야 되기 때문
cnt[i] = cnt[i-1] + cnt[i]- 정렬
- DATA 원본과 같은 Temp를 만들고,
- Temp에 가장 마지막 인덱스(N)를 삽입 후 counts[N]을 하나 감소시킨다.
- 그 다음 인덱스 (N-1)를 삽입 후 conts[N-1]을 하나 감소시킨다.
N = 6 # 경우의 수
K = 9 # 가장 큰 값
data = [7, 2, 4, 5, 2, 3] # 0 ~ 9, K = 9
counts = [0] * (K+1)
temp = [0] * N # 정렬된 결과 저장
#counts 배열에 기록하기
for x in data: counts[x] += 1
#counts 배열에 기록하기, 인덱스 번호를 이용
for x in range(0, len(data)):
counts[data[i]] += 1
# counts 누적합 구하기
for i in range(1,K+1): counts[i] += counts[i-1]
# data의 마지막 원소부터 정렬하기
for i in range(N-1, -1, -1): #N-1 -> 0번 인덱스 counts[data[i]] -= 1 #개수를 인덱스로 변환(남은 개수 계산) temp[ counts[data[i]] ] = data[i] print(*temp) # 원래 for문 밖에 있어야함, 과정을 보기위해 넣어둠왜 마지막 원소부터 하는가? 안정된 결과를 위해서 stable sort(안정정렬)
만약 첫 원소부터 하면, 1(a) 3 1(b) 2 1(c) 4 1(d) 이렇게 있을 때 1이 abcd 순으로 정렬되는 것이 아니라 dcba 순으로 나와버리게 된다. 같은 1이라도 순서를 안정적으로 고려해야된다.
누적하는것과 마지막 원소부터 하는 프로세스 ⇒ 안정정렬을 위함
baby-gin Game
3장이 연속된 번호 ⇒ run
3장이 동일한 번호 ⇒ triplet
6장 중 run 또는 triplet로만 구성 ⇒ baby-gin
어떻게 입력 받을 것인가?
667767은 (666,777)
054060 (456, 000)
101123 ( x)
어떻게 접근 할 것인가?
완전 검색 Exaustive Search
- 알고리즘의 종류가 아니고, 기법 중 하나
- 문제의 해법으로 생각할 수 있는 모든 경우의 수를 나열해보고 확인하는 기법
- Brute-force 또는 generate-and-test 기법 이라고 하기도 함
- 모든 경우의 수를 테스트 한 후, 최종 해법을 도출
- 일반적으로 경우의 수가 상대적으로 작을 때 유용함
특징
모두 경우의 수 생성 및 테스트 ⇒ 수행 속도 느림 ⇒ 해답 찾아내지 못할 확률 적음
주어진 문제를 풀 때, 완전 검색으로 접근하여 해답 도출 ⇒ 성능 개선을 위해 다른 알고리즘 사용
방법
- 고려할 수 있는 모든 경우의 수 생성하기
- 6개의 숫자로 만들 수 있는 모든 숫자 나열(중복 포함)
- 예) 입력으로 [2,3,5,7,7,7]을 받았을 때, 아래와 같이 순열을 생성할 수 있다.
2 3 5 7 7 7 2 3 7 8 7 7 ... 7 7 7 5 3 2 => 6! - 해답 테스트하기
- 앞의 3자리와 뒤의 3자리를 잘라 run, triplet 여부를 테스트, 최종적으로 baby-gin 판단
순열은 어떻게 생성하지?
순열
-서로 다른 것들 중 몇개를 뽑아서 한 줄로 나열하는 것
서로 다른 n개 중 r개를 택하는 순열은 nPr = n! 로표현
동일한 숫자가 포함되지 않았을 때, 각 자리 수 별로 loop을 이용해 구현
# 한계가 명확한 방법
for i1 in range(1,4):
for i2 in range(1,4):
if i2 != i1: for i3 in range(1,4): if i3 != i1 and i3 != i2: print(i1,i2,i3)
재귀를 이용할 때 이 방법을 대체 할 수 있다.탐욕 Greedy 알고리즘 < = > 완전 검색
- 최적해를 구하는데 사용되는 근시안 적인 방법
- 여러 경우 중 하나를 결정할 때 마다 가장 최적이라고 생각되는 것을 선택해 나가는 방식으로 진행하여 최종적인 해답에 도입한다.
- 각 선택의 시점에서 이루어지는 결정 = 지역적으로는 최적
but 그 선택들을 계속 수집하여 최종적이 해답 만들었다 ≠ 최적이다
- 일반적으로, 머릿속에 떠오르는 생각을 검증 없이 바로 구현하면 Greedy 접근
- 한 큐에 해결해버리겠다~! 하는 것, 되는 것도 있고 안 되는 것도 있음.
동작 과정
- 해 선택 : 현재 상태에서 부분 문제의 최적(가장 좋은) 해 구하기 → 부분해집합(Solution Set)에 추가한다.
- 실행 가능성 검사 : 새로운 부분해 집합이 실행 가능한지를 확인한다. = 곧, 문제의 제약 조건을 위반하지 않는지 검사
- 해 검사 : 새로운 부분해 집합이 문제의 해가 되는지 확인, 아직 전체 문제의 해가 완성되지 않았다면 다시 1번부터 실행
예시 - 거스름돈 줄이기
어떻게 하면 손님에게 거스름돈으로 주는 지폐와 동전의 개수를 최소한으로 줄일 수 있을까?
- 500, 100 10 동전
800원을 최소한의 동전 = 500 100 100 100
- 500 400 100 10 동전
그리디를 쓰면 500 100 100 100 으로 흘러감
but 800엔을 최소한의 동전 = 400 400
- 가장 좋은 해 선택,
- 단위가 큰 동전으로만 거스름돈 만들면, 동전의 갯수가 줄어든다
- 가장 큰 동전을 하나 골라 거스름돈에 추가한다.
풀이
- run 조사 후 run 데이터 완전 삭제
ex) 44345
counts : 141 → 030 (가능)
ex) 333456
counts : 3111 → 2001 (불가능) (그리디 방법 실패)
- triplet 조사 후 triplet 데이터 완전 삭제
ex) 44345
counts : 141 → 111 (가능)
ex) 333456
counts : 3111 → 0111 (가능) (그리디 방법 성공)
구현 예
num = 4456789 # Baby Gin 확인 할 6자리 수
c = [0] * 12 # 6자리 수로부터 각 자리 수를 추출하여 개수를 누적할 리스트
#마지막에 2칸을 더 추가해서 더미데이터로 쓸 예정이기 때문 0~9 + 2 = 12개
for i in range(6):
c[num % 10] += 1 # 1의 자리수를 구하기 = 마지막 인덱스부터 진행된다.
num //= 10
# num의 자리수를 모른다면?
for 대신에 while num > 0: i = 0
while i < 10:
if c[i] > = 3: #triplete 조사 후 데이터 삭제
c[i] = 3
tri += 1
continue
# if i <=7 조건을 넣는 대신, cnt를 2개 더 추가해놓는거로 해결함, 연산을 줄이기 위함
if c[i] >= 1 and c[i+1] >= 1 and c[i+2] >= 1 : # run 조사 후 데이터 삭제
c[i] +=1
c[i+1] += 1
c[i+2] += 1
run += 1
continue # run 조사 후 같은자리에서 다시 검사하기 위해 continue
i += 1
if run + tri == 2: print('Baby Gin')
else : print("Lose")자주 실수하는 오답
- 입력받은 숫자를
정렬한 후, 앞뒤 3자리씩 끊어서 run 및 triplet을 확인하는 방법을 고려할 수도 있다. - 예) [6,4,4,5,4,4] : 정렬하여[4,4,4,4,5,6] 이니까 baby여부 확인 가능
예) [1,2,3,1,2,3] : 정렬하면 [1,1,2,2,3,3] 이니까 baby 확인 실패
추가로 배운 것
- N개 :
[0] * Nvs
마지막 인덱스가 N :
[0] * (N+1) - 완전 검색 + 가지치기 = 백트래킹 = A형의 목적
- 카운팅 정렬의 합을 누적시켜가는 방법을 이용해
구간합 구하는 공식으로 쓸 수 있다.for i in range(1,K+1): counts[i] += counts[i-1] counts[i] 에 들어있는 값 = i번째 까지의 합기본 방법 만약 3개의 구간에 대한 합이 필요하다? [1,2,3,4,5] 이렇게 있을 때 1+2+3 = 6 2+3+4 = 9 6(n번째 까지의 합) + 4(n+1 값) - 1(n-2 값) = 9누적 합 이용한 방법 counts[i] = i 까지를 모두 더한 값 counts[i-3] = i-3 까지 모두 더한 값 counts[i] - counts[i-2] = i, i-1, i-2 다 더한 값 => O(n)
'TIl' 카테고리의 다른 글
| 이진탐색, 선택정렬 (0) | 2024.02.02 |
|---|---|
| 2차원 배열 , 부분집합 (0) | 2024.01.31 |
| 알고리즘 1 (1) | 2024.01.29 |
| 02 PJT (1) | 2024.01.26 |
| OOP 2 (1) | 2024.01.25 |
