패턴 매칭
찾고자 하는 문자열 패턴의 길이 m, 총 문자열 길이 n
- 고지식한 알고리즘 Brute Force $O(mn)$
- kmp 알고리즘 $O(n)$
- 카프-라빈 알고리즘: $O(n)$
- 보이어-무어 알고리즘 $O(MN)$(최악의 경우)~ $\omega(N)$(최소한에도 이정도 연산은 이루어진다)
고지식한 알고리즘 Brute Force
본문 문자열을 처음부터 끝까지 차례대로 순회하면서 패턴내의 문자들을 일일이 비교하는 방식으로 동작
알고리즘 설명
하나씩(i=0,j=0) 비교하는 중 다른 패턴(찾고자 하는 패턴이 아닌)이 보이게 되면
→ 한 칸 밀고(i=1,j=0) 다시 비교 해서 반복
p = "is" #찾을 패턴
t = "this is a book~!" #전체 텍스트
M = len(p) #찾을 패턴의 길이
N = len(t) #전체 텍스트의 길이
def BruteForce(p,t):
i = 0 # t의 인덱스
j = 0 #p의 인덱스
#else를 쓰지 않고 증가 하는것을 쓰기 위해 사용
while j <m and i <N:
if t[i] != p[j]:
i = i - j
j = -1
i = i + 1
j = j + 1
if j == M: return i-M # 검색 성공
else:return -1 # 검색 실패시간 복잡도 : $O(MN)$
최악의 경우 텍스트의 모든 위치에서 패턴을 비교해야 하므로
길이가 10000인 문자열에서 길이 80인 패턴을 찾는다고 할 때, 최악의 경우 약 10,000*80 = 800,000 번의 비교가 일어난다
⇒ 비교횟수를 줄일 수 없을까?
KMP 알고리즘
세 사람 이름 앞 글자 따서 온 알고리즘
- 불일치가 발생한 텍스트 String의 앞 부분에 어떤 문자가 있는지를 미리 알고 있으므로, 불일치가 발생한 앞 부분에 대하여 다시 비교하지 않고 매칭을 수행
-
- 패턴을 전처리하여 배열 next[M]을 구해서 잘못된 시작을 최소화함
- next[M] : 불일치가 발생했을 경우 이동할 다음 위치
- 패턴을 전처리하여 배열 next[M]을 구해서 잘못된 시작을 최소화함
- 시간 복잡도 : $O(M+N)$
아이디어 설명
- 텍스트에서 abcdabc까지는 매치되고, e에서 실패한 상황 패턴의 맨앞의 abc와 실패 직전의 abc는 동일함을 이용할 수 있다.
- 실패한 텍스트 문자와 P[4]를 비교한다.

- 매칭이 실패했을 때 돌아갈 곳을 계산한다.

보이어-무어 알고리즘
- 오른쪽에서 왼쪽으로 비교
- 대부분의 상용 소프트웨어에서 채택하고 있는 알고리즘
- 보이어-무어 알고리즘은 패턴에 오른쪽 끝에 있는 문자가 불일치 하고 이 문자가 패턴 내에 존재하지 않는 경우, 이동 거리는 무려 패턴의 길이 만큼이 된다.

오른쪽 끝에 있는 문자가 불일치 하고 이 문자가 패턴 내에 존재할 경우

예시

- 앞의 두 매칭 알고리즘들의 공통점 : 텍스트 문자열의 문자를 적어도 한번씩 훑는다는 것 ⇒ 최선의 경우에도 $\omega(n)$
- 보이어-무어 알고리즘은 텍스트 문자를 다 보지 않아도 된다
- 발상의 전환 : 패턴의 오른쪽부터 비교한다
- 최악의 경우 수행시간 : $O(mn)$
- 입력에 따라 다르지만, 일반적으로 $O(n)$보다 시간이 덜 든다
참고
bit 열의 암호화
배타적 논리합(exclusive-or) 연산 사용

키가 0이면 그대로 유지, 키가 1이면 반전
암호화 : 평문에다가 키를 대고 배타적 논리합을 실행하면 암호문이 나옴
복호화 : 암호문에다가 키를 대고 배타적 논리합을 실행하면 평문이 나옴
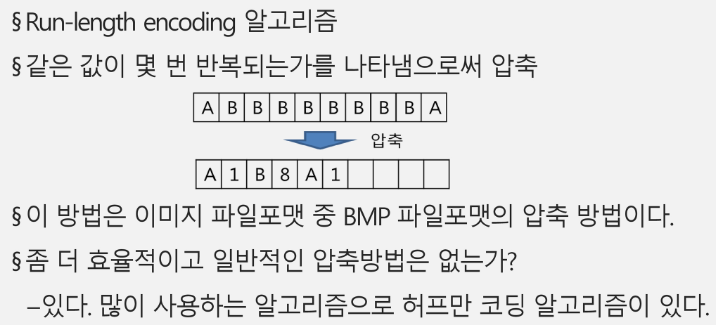
문자열 압축
저장소의 크기를 줄이며 정확한 정보를 저장하는 방법은?
아스키 코드
a
b
은
61 0d 0A 62 로 표현됨
a CR LF b
CRLF는 텍스트 파일을 CRLF로 저장하는 방식임을 표현하는 것
(파이참은 오른쪽 하단에서 확인 가능)0x03 :
0000 0011
0x30 :
0011 0000
header와 footer을 붙어서 보낸다.팁
온라인 강사님 긱스포긱스? 에서 자주 참고를 하신다고 함
'TIl' 카테고리의 다른 글
| DP, DFS (1) | 2024.02.13 |
|---|---|
| Stack, recursive F(), Memoization (1) | 2024.02.07 |
| String (1) | 2024.02.05 |
| 알고리즘 풀이 (0) | 2024.02.02 |
| 이진탐색, 선택정렬 (0) | 2024.02.02 |


