TIl

Queue

아크몽 2024. 2. 15. 22:02

큐

스택과 마찬가지로 삽입과 삭제의 위치가 제한적인 자료구조
- 큐의 뒤에서는 삽입만 하고, 큐의 앞에서는 삭제만 이루어지는 구조
선입선출구조(FIFO : First In First Out)
- 큐에 삽입한 순서대로 원소가 저장되어, 가장 먼저 삽입(First In)된 원소는 가장 먼저 삭제(First Out) 된다.

선입선출, 후입선출 둘 다 `꺼내는 걸` 기준으로 본다.

front : 마지막으로 꺼내진(삭제된) 위치

rear : 마지막으로 저장된 위치

스택과 다르게 입,출구가 존재한다

큐의 기본 연산

삽입 : enQueue

삭제 : deQueue

큐의 주요 연산

enQueue(item) : 큐의 뒤쪽(rear 다음)에 원소를 삽입하는 연산
deQueue() : 큐의 앞쪽(front)에서 원소를 삭제하고 반환하는 연산
createQueue() : 공백 상태의 큐를 생성하는 연산
isEmpty() : 큐가 공백상태인지를 확인하는 연산
isFull() : 큐가 포화상태인지를 확인하는 연산
Qpeek() : 큐의 앞쪽(front)에서 원소를 삭제 없이 반환하는 연산

연산과정

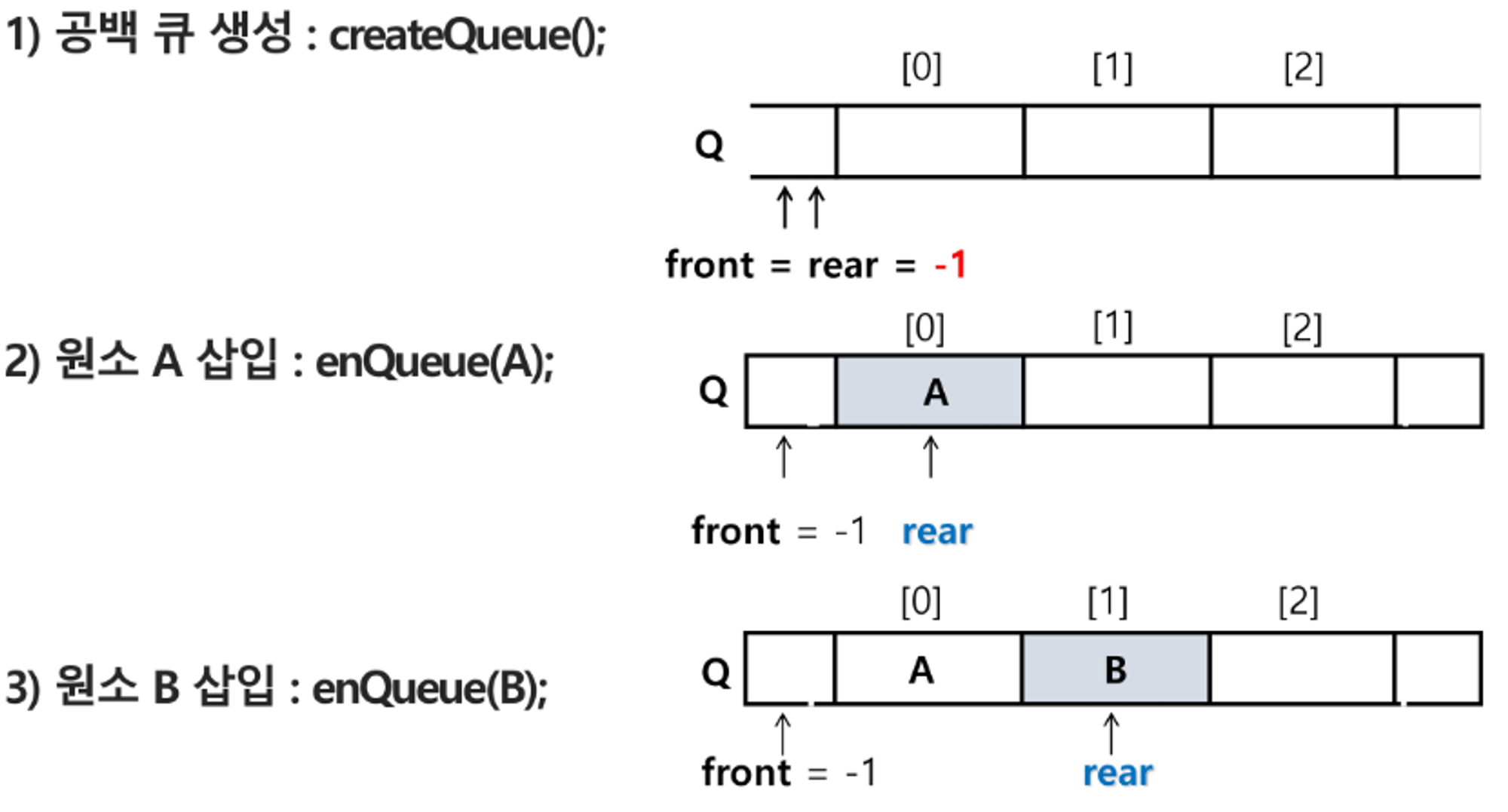
rear 가 증가되고 나서 값 들어간다

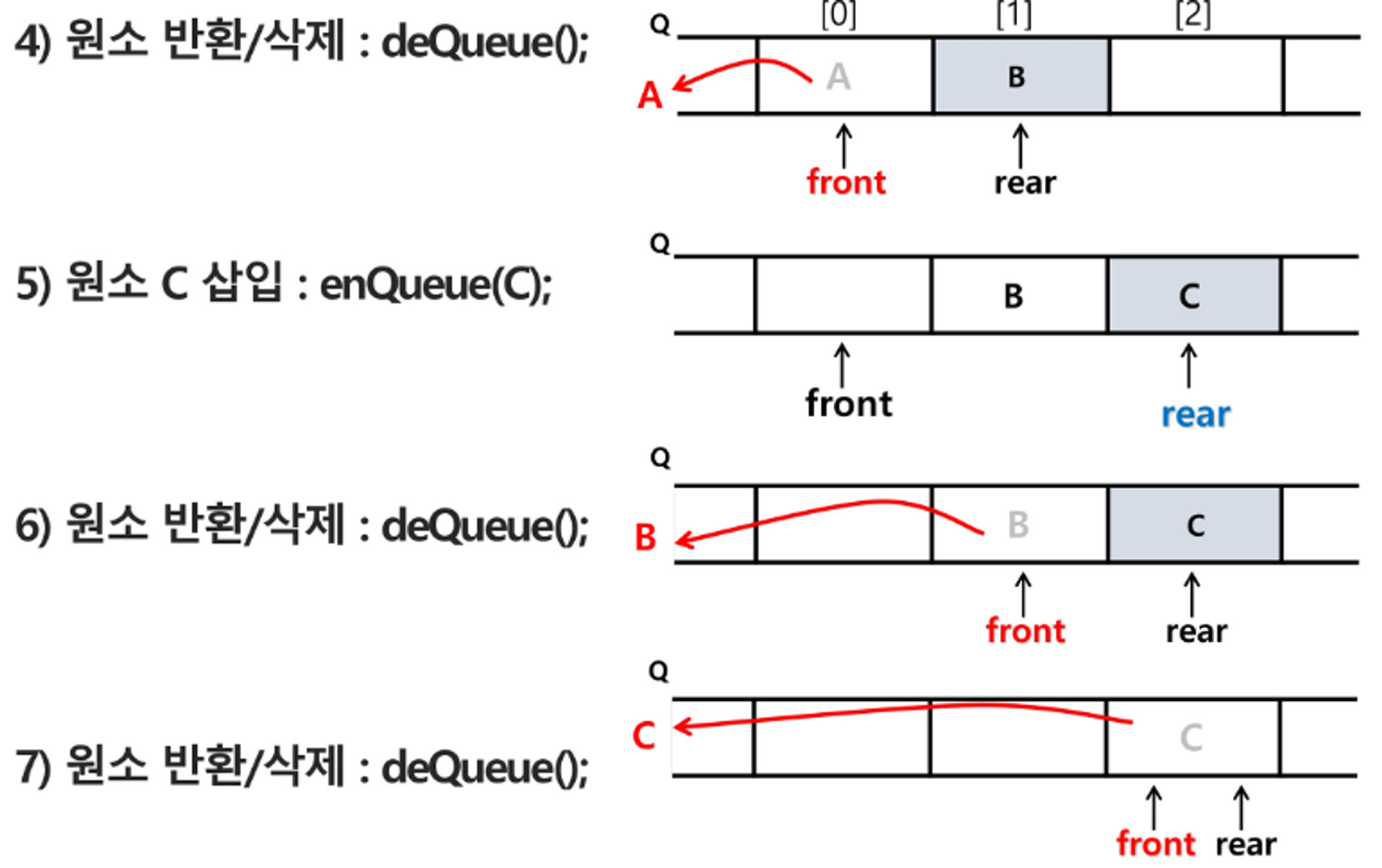
상기된 절차가 끝나면 font == rear ⇒ isEmpty 상태

rear 가 마지막 인덱스(n-1) 에 도달했다? ⇒ isFull 상태

front 와 rear가 같은 자리를 가르킨다? = 마지막으로 저장된게 꺼내졌어

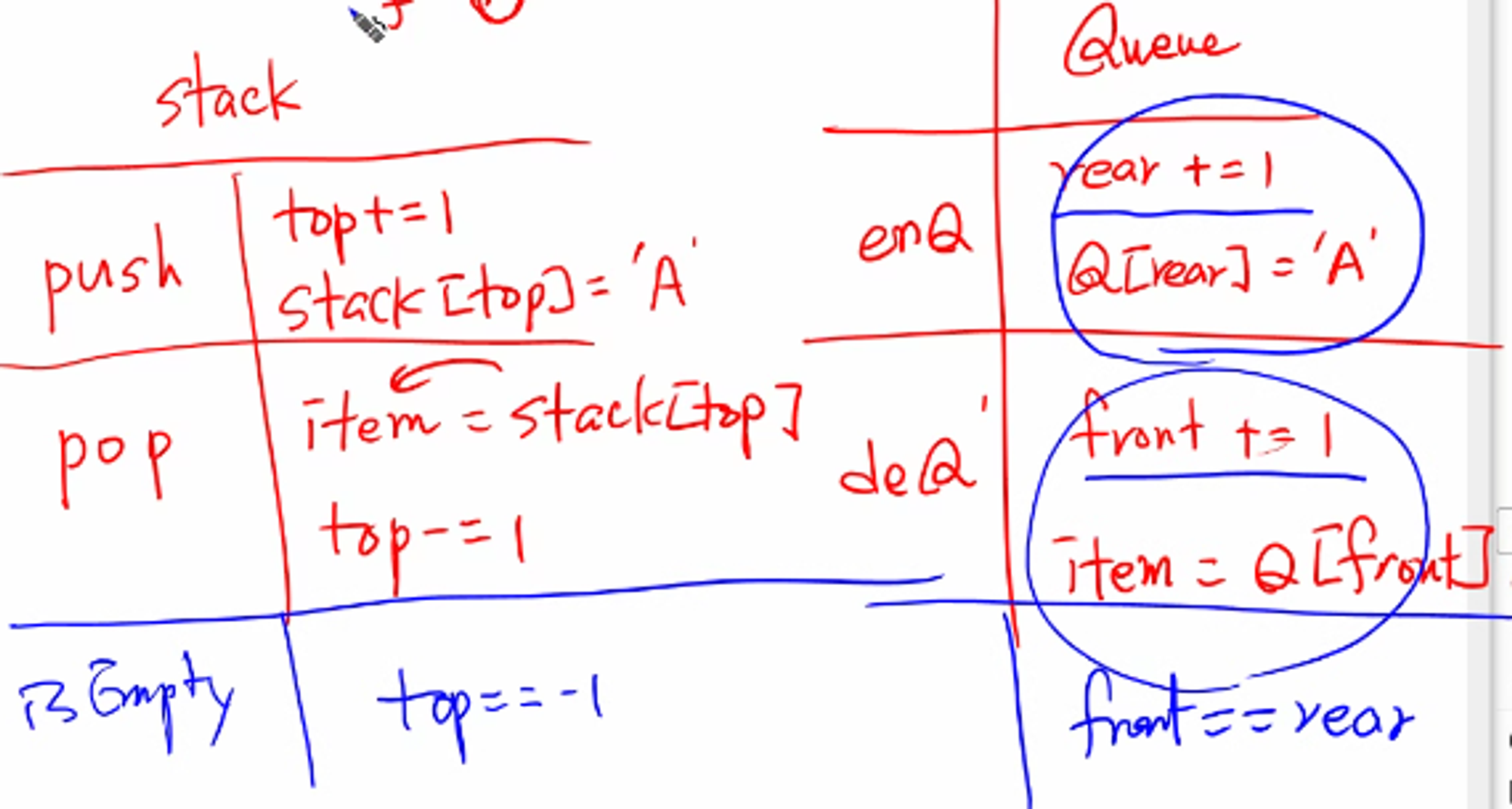
선형큐

1차원 배열을 이용한 큐
- 큐의 크기 = 배열의 크기
- front : 마지막으로 삭제된 인덱스 (=ppt 엔 저장된 첫 번째 원소의 인덱스)
- rear : 저장된 마지막 원소의 인덱스
상태 표현
- 초기 상태 : front = rear = -1
- 공백 : front == rear
- 포화 : rear== n-1 (n : 배열의 크기, n-1 : 배열의 마지막 인덱스)
  포화상태에 도달하면 안된다 == 스택을 크게 잘 잡아야된다.
초기 공백 큐 생성
- 크기 n인 1차원 배열 생성
- front와 rear를 -1로 초기화

삽입 enQueue(item)

마지막 원소 뒤에 새로운 원소를 삽입하기 위해
- 1) rear 값을 하나 증가시켜 새로운 원소를 삽입할 자리를 마련
- 2) 그 인덱스에 해당하는 배열원소 Q[rear]에 item을 저장
```
def enQueue(item):
  global rear
  if isFull(): print("Queue_Full") # 디 버깅용 코드, 이 조건으로 들어오면 안된다
  else:
    rear <- rear + 1;
    Q[rear] <- item;
```

삭제 : deQueue()

가장 앞에 있는 원소를 삭제하기 위해
- 1) front 값을 하나 증가시켜 큐에 남아있는 첫 번째 원소 이동
- 2) 새로운 첫 번째 원소를 리턴 함으로써 삭제와 동일한 기능함
```
deQueue()
  if (isEmpty()) then Queue_Empty();
  else {      front <- front + 1;      return Q[front];
  }
```

공백상태 및 포화상태 검사

공백 상태: front == rear

포화 상태 : rear == n-1 (n: 배열의 크기, n-1 : 배열의 마지막 인덱스)

def isEmpty():
  return front == rear
def isFull():
  return rear == len(Q) - 1

검색 : Qpeek()

가장 앞에 있는 원소를 검색하여 반환하는 연산
현재 front의 한자리 뒤(front +1)에 있는 원소, 즉 큐의 첫 번째에 있는 원소를 반환

def Qpeek():
  if isEmpty() : print('Queue_Empty')
  else: return Q[front+1]

작동 코드 예시-인덱스

# front, rear 이용
Q = [0] * 10
front = rear = -1

# enQ
rear += 1
Q[rear] = 1
rear += 1
Q[rear] = 2
rear += 1
Q[rear] = 3
print('before',front, rear,Q) # -1 2 [1, 2, 3, 0, 0, 0, 0, 0, 0, 0]
print(f'peek : {Q[front+1]}') # Qpeek # 1


# deQ
while front != rear:   front += 1   print(Q[front])
print('after',front, rear,Q) #  2 2 [1, 2, 3, 0, 0, 0, 0, 0, 0, 0]

중요한점 - 인덱스 형식

front 와 rear은 더해지기만 한다. == 스택의 길이가 굉장히 길어야한다.
더해지기만 함 == 스택은 실제로 제거되는것이 아니다.
실제로 제거 X == 메모리 낭비, BUT 낭비한채로 둔다.

작동코드 예시-리스트

# 작동 느림 (= 시간복잡도 복잡) ( pop(0)를 쓰기 때문)
Q = []

# enQ
Q.append(1) # O(1)
Q.append(2)
Q.append(3)
print(Q) # [1,2,3]
print(f'peak : {Q[0]}')

# deQ
while Q:   print(Q.pop(0)) # O(n) == 비효율적이다. => deque(덱)를 사용하면 O(1)
print(Q) # []

원형 큐

선형 큐 이용시의 문제점 - 잘못된 포화상태 인식

선형 큐를 이용하여 원소의 삽입과 삭제를 계속할 경우,
배열의 앞 부분에 활용할 수 있는 공간이 있음에도 불구하고,

rear=n-1 인 상태 즉, 포화 상태로 인식하여 더 이상의 삽입을 수행하지 않게 됨

해결방법 1 쓰지말것

매 연산이 이루어질 때마다 저장된 원소들을 배열의 앞 부분으로 모두 이동시킴
⇒ 원소 이동에 많은 시간이 소요 == 큐의 효율성이 급격히 떨어짐

해결방법 2 원형 큐

1차원 배열을 사요하되, 논리적으로는 배열의 처음과 끝이 연결되어 원형 형태의 큐를 이룬다고 가정하고 사용
원형 큐의 논리적 구조

원형 큐의 구조

초기 공백상태 : front == rear = 0 (선형 큐와의 차이점)
index의 순환
- front 와 rear의 위치가 배열의 마지막 인덱스인 n-1를 가리킨 후, 그 다음에는 논리적 순환을이루어 배열의 처음 인덱스인 0으로 이동해야 함
- 이를 위해 나머지 연산자 mod(%) 를 사용함
front 변수
- 공백 상태와 포화 상태 구분을 쉽게 하기 위해 front가 있는 자리는 사용하지 않고 항상 빈자리로 둠
삽입 위치 및 삭제 위치

원형 큐의 연산 과정

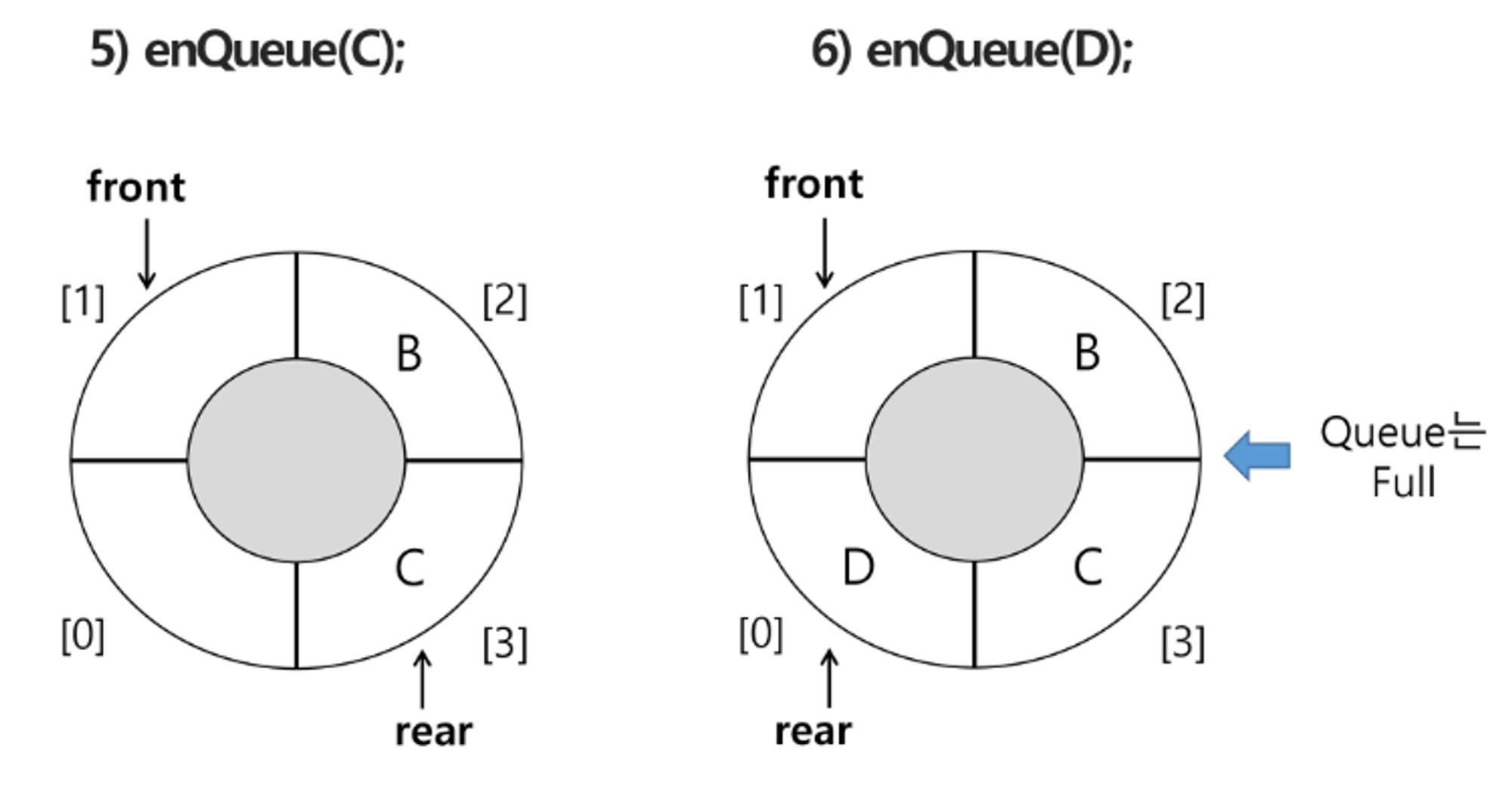
초기 공백 큐 생성

크기 n인 1차원 배열 생성
front와 rear를 0으로 초기화

공백상태 및 포화상태 검사 :

공백상태 : front ==rear

포화상태 : 삽입할 rear의 다음 위치 == 현재 front

(rear + 1) mod n == front

def isEmpty():
  return front == rear

def isFull():
  return (rear+1) % len(cQ) == front
# 만약 길이가 4 라면 (r+1) % 4

front == (rear+1) % N

삽입 : enQueue(item)

마지막 원소 뒤에 새로운 원소를 삽입하기 위해
1) rear 값을 조정하여 새로운 원소를 삽입할 자리를 마련함 :
rear ← (rear + 1) mod n;

2) 그 인덱스에 해당하는 배열원소 cQ[rear]에 item을 저장
```
def enQueue(item):
  global rear
  if isFull():
    print('큐가 풀이야')
  else:
    rear = (rear + 1) % len(cQ)
    cQ[rear] = item
```

삭제 : deQueue(), delete()

가장 앞에 있는 원소를 삭제하기 위해
1) front 값을 조정하여 삭제할 자리를 준비한다

2) 새로운 front 원소를 리턴 함으로써 삭제와 동일한 기능을 한다.
```
def deQueue():
  global front
  if isEmpty():
    print('큐가 비었어')
  else:
    front = (front +1 ) % len(cQ)
    return cQ[front]
```

연결 큐

단순 연결 리스트(Linked List)를 이용한 큐

큐의 원소 : 단순 연결 리스트의 노드
큐의 원소 순서 : 노드의 연결 순서, 링크로 연결되어 있음
front: 첫 번째 노드를 가리키는 링크
rear : 마지막 노드를 가리키는 링크

상태표현

초기 상태 : front = rear = null
공백상태 : front = rear = null

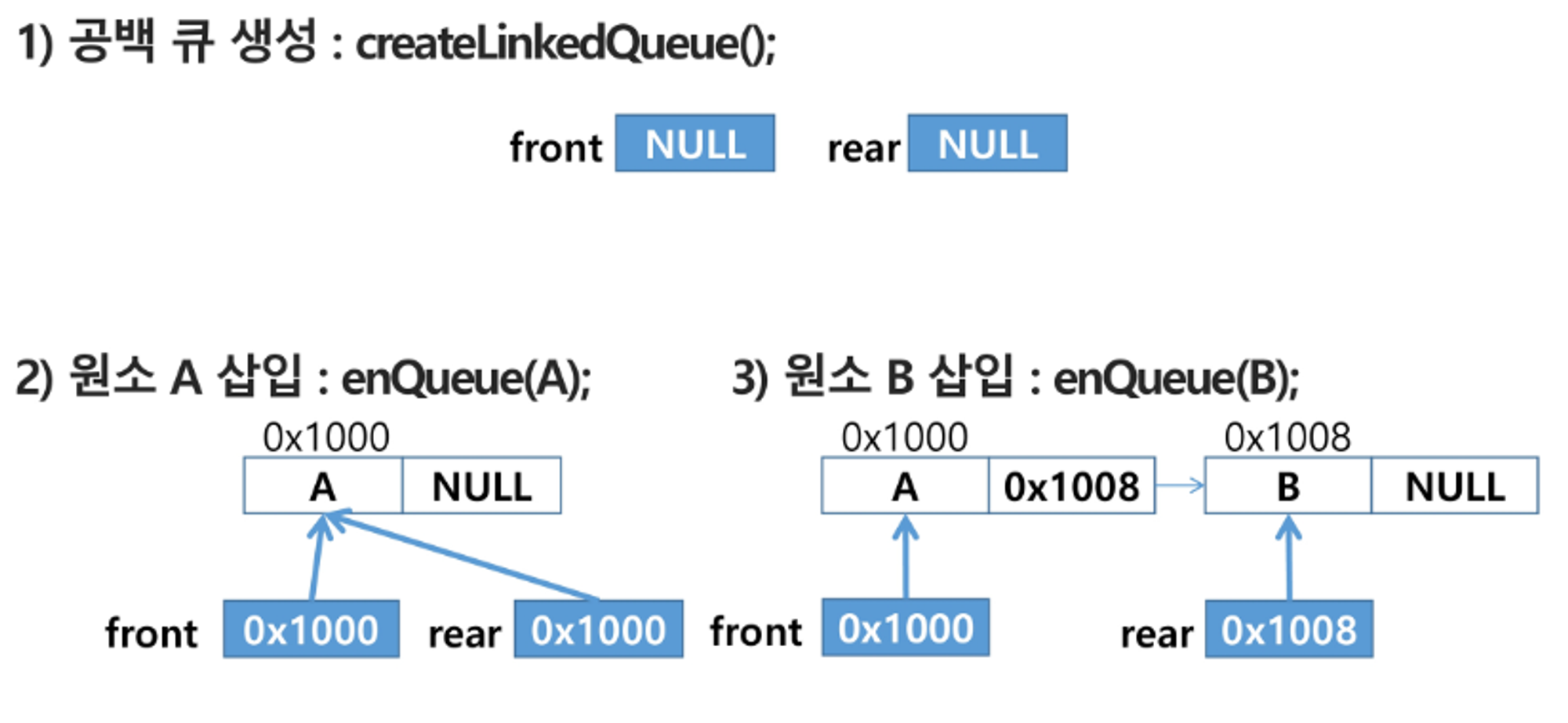
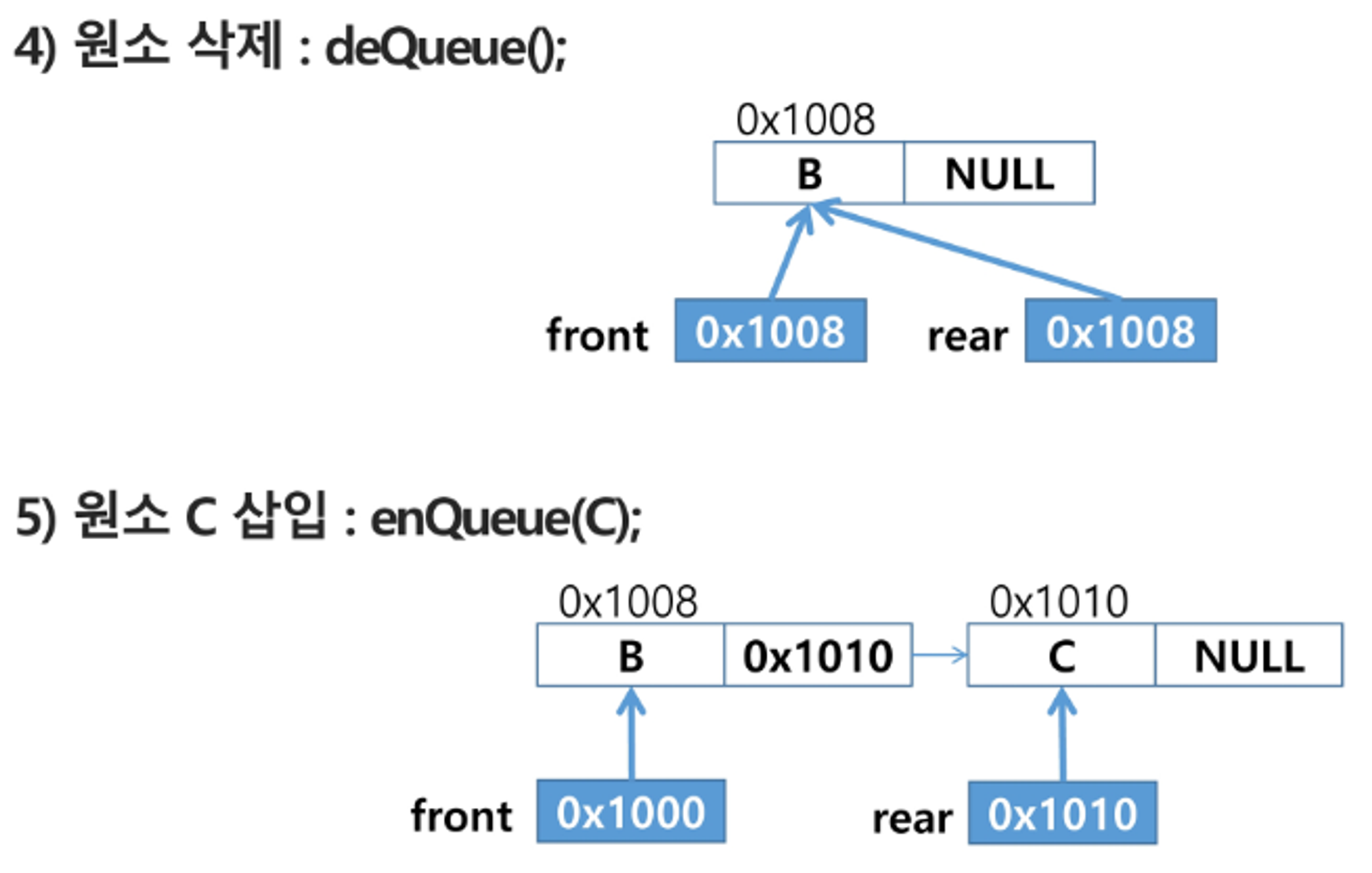
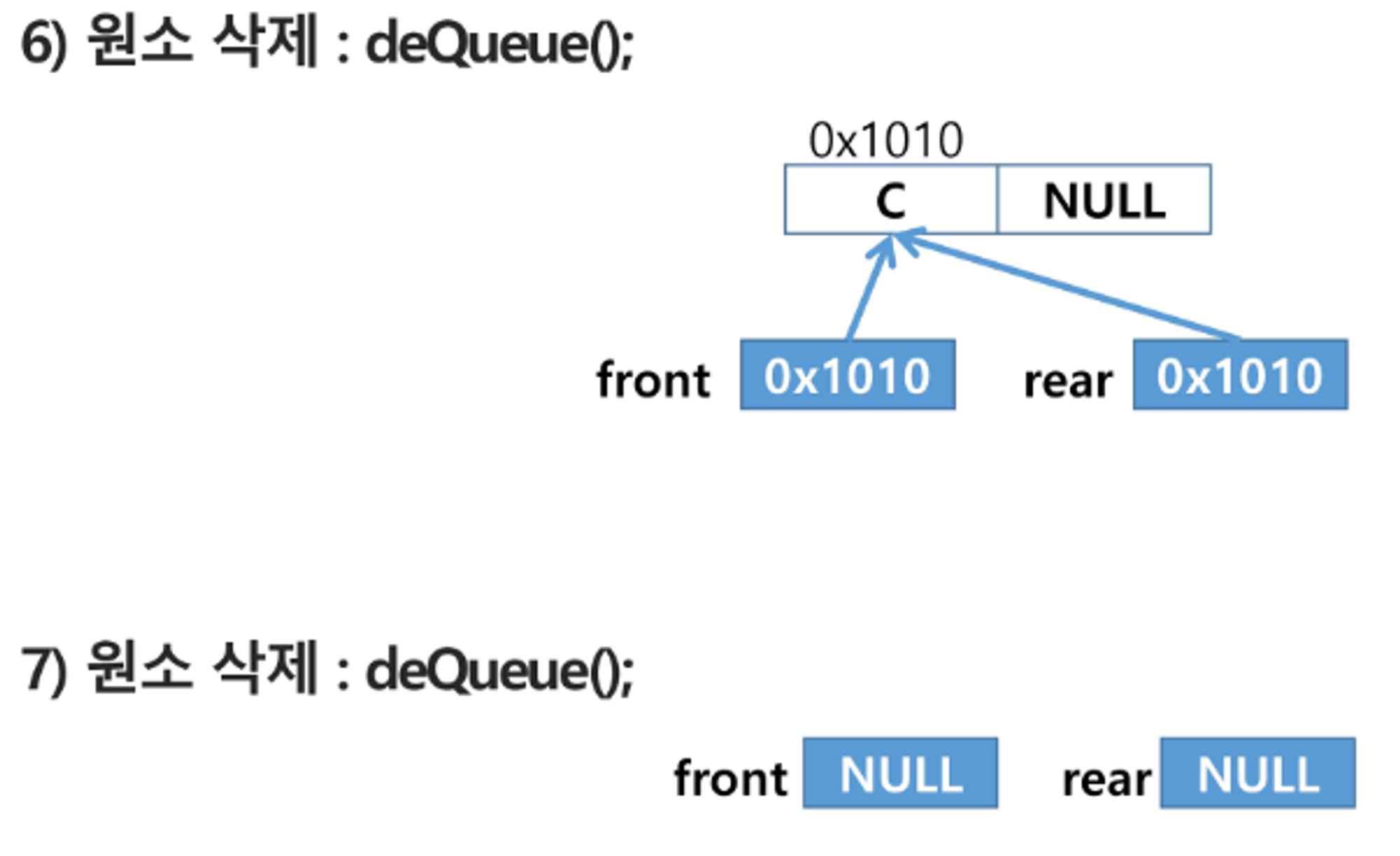
deque (덱)

컨테이너 자료형 중 하나
양쪽 끝에서 빠르게 추가와 삭제를 할 수 있는 리스트류 컨테이너
이중 연결 리스트 를 사용하기 때문에 양쪽에 접근이 가능하다.
연산
- append(x) : 오른쪽에 x 추가
- popleft() : 왼쪽에서 요소를 제거하고 반환, 요소가 없으면 indexError
```
from collections import deque

q = deque()
q.append(1) #enqueue()
t = q.popleft() # dequeue()
```

우선순위 큐 Priority Queue

우선순위를 가진 항목들을 저장하는 큐
FIFO 순서가 아니라 우선순위가 높은 순서대로 먼저 나가게 된다.
heap 메모리 자료형 사용, 트리에 사용됨

우선순위 큐의 적용 분야

시뮬레이션 시스템
네트워크 트래픽 제어
운영체제의 테스크 스케줄링

우선순위 큐의 구현

배열 이용
리스트 이용

우선순위 큐 기본 연산

삽입, 삭제

배열을 이용하여 우선순위 큐 구현

배열을 이용하여 자료 저장
원소를 삽입하는 과정에서 우선순위를 비교하여 적절한 위치에 삽입하는 구조
가장 앞에 최고 우선순위의 원소가 위치하게 됨

문제점

배열을 사용하므로, 삽입이나 삭제 연산이 일어날 때 원소의 재배치가 발생함
이에 소요되는 시간이나 메모리 낭비가 큼

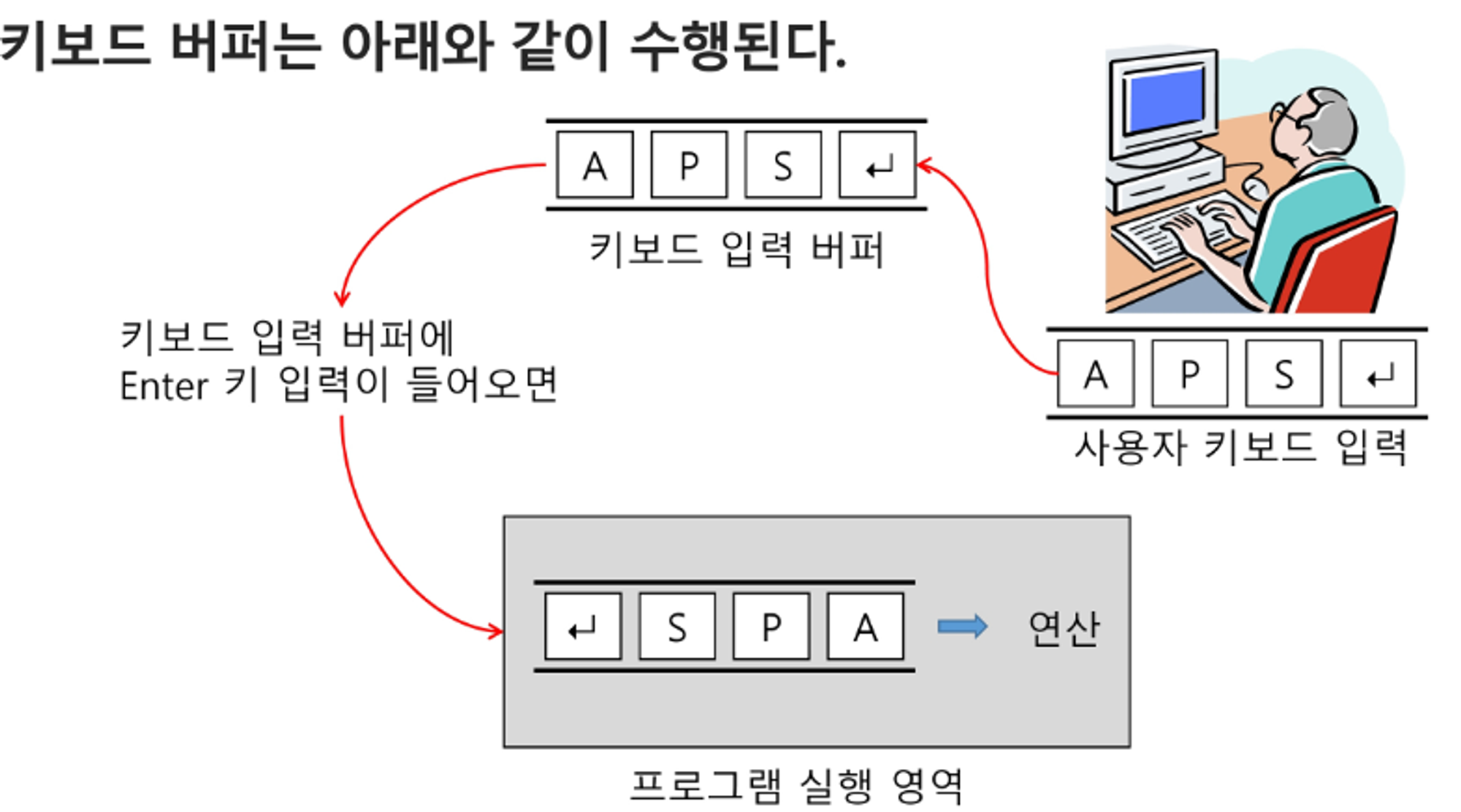
버퍼

데이터를 한 곳에서 다른 한 곳으로 전송하는 동안 일시적으로 그 데이터를 보관하는 메모리의 영역
버퍼링 : 버퍼를 활용하는 방식 또는 버퍼를 채우는 동작을 의미한다.

버퍼의 자료 구조

버퍼는 일반적으로 입출력 및 네트워크와 관련된 기능에서 이용된다.
순서대로 입력/출력/전달되어야 하므로 FIFO 방식의 자료구조인 큐가 활용된다.

Queue

Queue

큐

선입선출, 후입선출 둘 다 꺼내는 걸 기준으로 본다.

큐의 기본 연산

큐의 주요 연산

연산과정

선형큐

삽입 enQueue(item)

삭제 : deQueue()

공백상태 및 포화상태 검사

검색 : Qpeek()

작동 코드 예시-인덱스

중요한점 - 인덱스 형식

작동코드 예시-리스트

원형 큐

선형 큐 이용시의 문제점 - 잘못된 포화상태 인식

원형 큐의 구조

원형 큐의 연산 과정

초기 공백 큐 생성

공백상태 및 포화상태 검사 :

front == (rear+1) % N

삽입 : enQueue(item)

삭제 : deQueue(), delete()

연결 큐

단순 연결 리스트(Linked List)를 이용한 큐

상태표현

deque (덱)

우선순위 큐 Priority Queue

우선순위 큐의 적용 분야

우선순위 큐의 구현

우선순위 큐 기본 연산

배열을 이용하여 우선순위 큐 구현

문제점

버퍼

버퍼의 자료 구조

선입선출, 후입선출 둘 다 `꺼내는 걸` 기준으로 본다.