TIl
BFS
아크몽
2024. 2. 16. 21:54
BFS 너비 우선 탐색 (Breath)
탐색 시작점의 인접한 정점들을 먼저 모두 차례로 방문
⇒방문했던 정점을 시작점으로 하여
⇒다시 인접한 정점들을 차례로 방문하는 방식
인접한 정점들에 대해 탐색을 한 후,
차례로 다시 너비우선탐색을 진행해야 하므로,
선입선출 형태의 자료구조인 큐를 활용함

이 순서대로 큐에 쌓인다.
실제 활용 : 출발해서 도착할때까지의 시간
A 가 1분걸렸다
B,C,D 는 A에서 1분을 더한다 1+1
EF는 B에서 1분을 더한다. 1+1+1, GHI는 D에서 1분을 더한다. 1+1+1
def BFS(G,v) # 그래프 G, 탐색 시작점 v visited = [0] * (n+1) # n: 정점의 개수 queue = [] # 큐 생성 queue.append(v) # 시작점 v를 큐에 삽입 while queue: t = queue.pop(0) if not visited[t]: # 방문되지 않은 곳이라면 visited[t] =True # 방문한 것으로 표시 visit(t) # 정점 t에서 할 일 for i in G[t]: # t와 연결된 모든 정점에 대해 if not visited[i]: # 방문되지 않은 곳이라면 queue.append(i) # 큐에 넣기
and 방문하지 않음 이 생략되어 있음
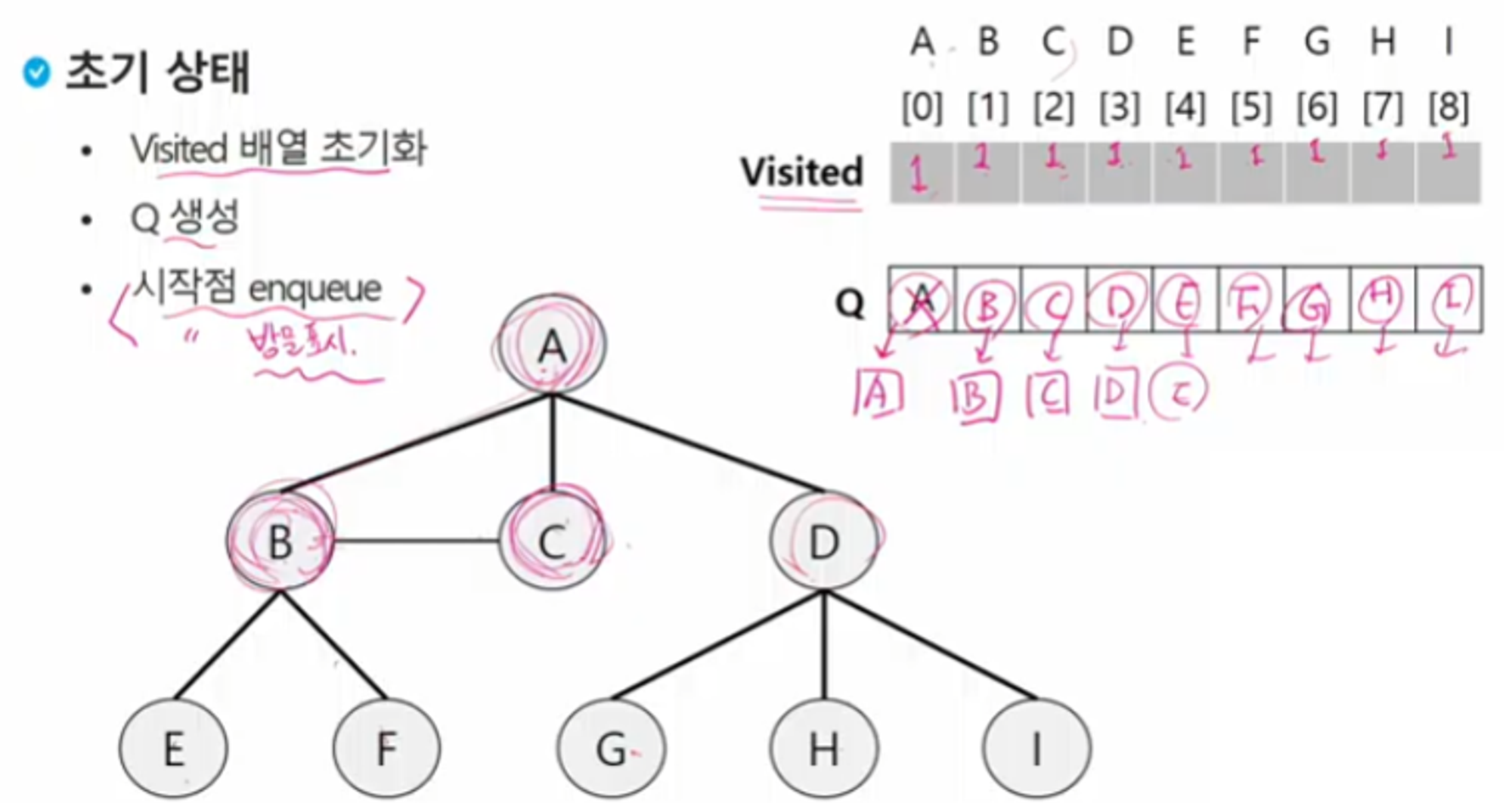
시작점과 방문표시가 동시에 진행된다.
시간 활용까지 사용한 예제

def BFS(G,v): # 그래프 G, 탐색 시작점 v visited = [0] * (n+1) # n: 정점의 개수 queue = [] # 큐 생성 queue.append(v) # 시작점 v를 큐에 삽입 visited[v] = True # 방문체크가 삽입과 같이 됨 == 기본틀과의 차이점 while queue: # 큐가 비어있지 않은 경우 t = queue.pop(0) # 큐의 첫번째 원소 반환 visit(t) # 정점 t에서 할 일 for i in G[t]: # t와 연결된 모든 정점에 대해 if not visited[i]: # 방문되지 않은 곳이라면 queue.append(i) # 큐에 넣기 visited[i] = visited[t] + 1 # n으로 부터 1만큼 이동
연습문제 3


1이 시작점이라면? 1-23-457-6
4가 시작정점이라면? 4 -26 -157 - 3
5가 시작정점이라면? 5 - 26-147-3
"""
V, E : V 1~V 까지 V개의 정점. E개의 간선
E개의 간선정보
7 8
1 2 1 3 2 4 2 5 4 6 5 6 6 7 3 7
"""
def bfs(s,N): # s : 시작정점 s, 노드 개수 N q = [] # 큐 visited = [0] * (N+1) # visited q.append(s) # 시작점 인큐 visited[s] = 1 # 시작점 방문표시 while q: # 큐가 비워질때까지... (남은 정점이 있으면) t = q.pop(0) # t에서 할 일일 print(t, end=' ') # 1 2 3 4 5 7 6 for i in adjl[t]: # t에 인접인 정점을 꺼내서 if visited[i] ==0: # 방문하지 않았네? q.append(i) # 인큐 visited[i] = 1 + visited[t] # 방문표시 print(visited) # [0, 1, 2, 2, 3, 3, 4, 3]
V, E = 7, 8
arr = [1, 2, 1, 3, 2, 4, 2, 5, 4, 6, 5, 6, 6, 7, 3, 7]
# 인접리스트
adjl = [[] for _ in range(V+1)] # [[], [2, 3], [1, 4, 5], [1, 7], [2, 6], [2, 6], [4, 5, 7], [6, 3]]
for i in range(E): n1, n2 = arr[i*2], arr[i*2+1] adjl[n1].append(n2) adjl[n2].append(n1) # 무방향 그래프
bfs(1, V)
bfs(4, V) #4 2 6 1 5 7 3 [0, 3, 2, 4, 1, 3, 2, 3]