반복과 재귀는 유사한 작업을 수행할 수 있다.
반복은 수행하는 작업이 완료될 때 까지 반복
- 루프( for, while 구조)
- 반복문은 코드를 n 번 반복을 구현
재귀는 주어진 문제의 해를 구하기 위해 동일하면서 더 작은 문제의 해를 이용하는 방법
- 하나의 큰 문제를 해결할 수 있는(해결하기 쉬운) 더 작은 문제로 쪼개고 결과들을 결합한다.
- 재귀 호출은 n중 for문을 구현
- ⇒ 재귀 함수로 구현
- 반복이 과도해지면 개발자가 피곤하다
재귀를 연습하기 전, 알아야 할 함수의 특징
- 함수 호출할 때, int 타입 객체를 전달하면 값만 복사된다. (int나 string 의 특징)
# main 함수의 x와, kfc함수의 x는 서로 다른 객체이다.
def main():
x = 3
kfc(x)
print(x)
def kfc(x):
x += 1- 함수가 끝나면, Main으로 되돌아 오는 것이 아닌, 해당 함수를 호출했던 곳으로 돌아온다.
def main():
x = 3
kfc(x+5)
print(x)
def kfc(x):
print(x)
x += 1
bts(x+5)
print(x)
def bts(x):
print(x)
# 8 14 9 3 출력 됨재귀 호출은 무한 재귀 호출이 발생할 수 있다. ⇒ 막는 것부터 시작
⇒ 기저조건(base case)가 필요하다
재귀호출이 여러개 나올 때 트리 ‘형태’로 나옴 (≠ 트리)
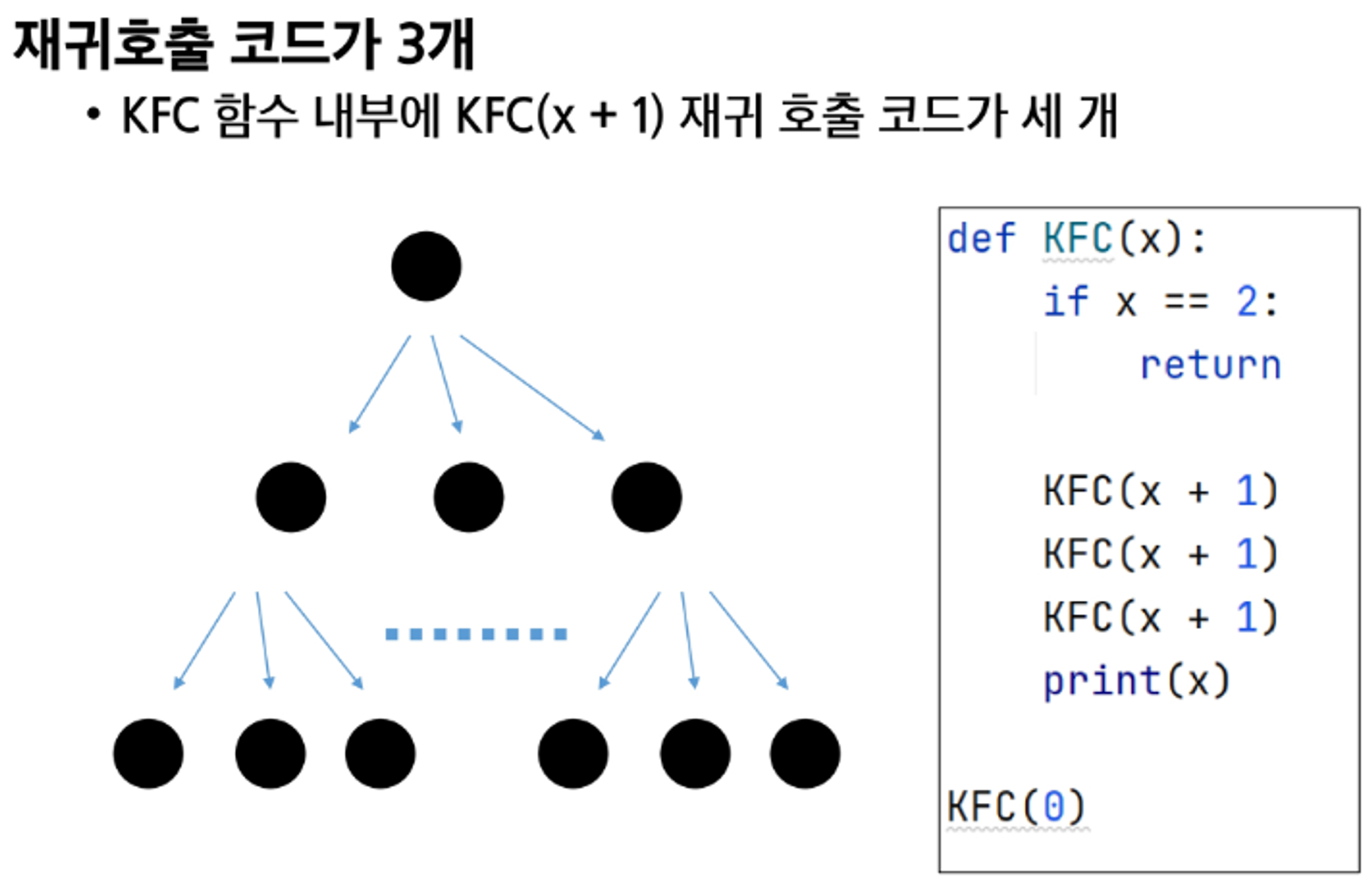
재귀호출이 3개니까 가지(branch)가 3개
기저조건이 ==2니까 깊이(level)이 2개
def run(level): if level ==2: return for i in range(3): # branch run(level+1)
run(0)순열
서로 다른 N개 에서, R개를 중복 없이, 순서를 고려하여 나열하는 것
예)
[0][1][2]로 구성된 3장의 카드가 다량으로 존재한다.
이 중에 2장을 뽑아 순열을 나열(중복 취급 X)
N x (N-1)
중복순열
서로 다른 N개에서, R개의 중복을 허용하고, 순서를 고려하여 나열하는 것
N x N 가지의 경우의 수
중복 순열 구현 원리
- 재귀호출을 할 때 마다, 이동 경로를
흔적으로 남긴다. - 가장 마지막 레벨에 도착했을 때 이동 경로(흔적)를 출력한다.
Path : 흔적 list, 전역 리스트로 초기화
# level 2 (0,1) branch 3 (0,1,2)
path = []
def funx(x): if x ==2: print(path) return for i in range(3): path.append(i) funx(x + 1) path.pop()
funx(0)순열 구현 원리
원래 순열은 중복을 취급하지 않음
- 중복 순열 코드를 작성한다.
- 중복을 제거하는 코드를 추가하면 ⇒ 순열 코드
중복을 제거하는 원리
- 전역리스트를 사용하면, 이미 선택했던 숫자인지 아닌지 구분할 수 있다.
- 이를 used 배열 or visited 배열 이라고 함 (DFS, BFS에 사용되는 것과 같이)
중복 제거 예시
0을 선택하고 재귀호출 한 후에는, 또 다시 0을 선택하지 못하도록 막아야 한다.
재귀 호출을 하기 직전, 이미 선택했던 숫자인지 아닌지 검사하는 코드가 필요함
순열 구현하기
- 이미 사용한 숫자인지 아닌지 구분하는 코드
만약 이미 사용한 숫자다? 재귀호출을 생략하는 코드를 추가
- 처음 사용하는 숫자라면? used에 기록을 해준다.
그리고 모든 처리가 끝나고 돌아왔다면? used에 기록을 지워준다.
path = []
used = [False, False, False]
def funx(x)
if x == 2:
print(path)
return
for i in range(3):
if used[i] == True : continue # 이미 사용한 숫자인지 아닌지 구분하는 코드
used[i] = True # 처음 사용하는 숫자 => 기록
path.append(i)
funx(x+1)
path.pop()
used[i] = False # 모든 처리가 끝났다 => 기록 지우기
funx(x)완전탐색 ( Brute-Force)
모든 가능한 경우를 모두 시도를 해서 정답을 찾아내는 것
예시 1) 주사위 3개 합이 10 이하
path = []
def perm(x,sum): global cnt if sum > 10: # 가지치기 return if x ==3: cnt += 1 # print(f'{path} : {sum}') return for i in range(1,7): path.append(i) perm(x+1, sum + i ) path.pop()
cnt = 0
perm(0,0)
print(cnt)예시2) A,J,Q,K 4종류의 카드들 중 5장을 뽑아 나열할 때, 같은 종류의 카드가 세 장 연속으로 나오는 경우의 수
card = ['a','k','q','j']
path = []
def same_card(): if path[0] == path[1] == path[2]: return True if path[1] == path[2] == path[3]: return True if path[2] == path[3] == path[4]: return True return False
def twistedpated(x): global cnt if x == 5: # 5장 뽑아야된다. if same_card(): cnt += 1 return for i in range(4): # 4종류의 카드 path.append(card[i]) twistedpated(x+1) path.pop()
cnt = 0
twistedpated(0)
print(cnt)'TIl' 카테고리의 다른 글
| Computing Thinking (3) | 2024.03.05 |
|---|---|
| 부분집합, 조합, 그리디 심화 (4) | 2024.02.28 |
| Start (1) | 2024.02.26 |
| Tree (0) | 2024.02.22 |
| Queue, BFS 보충 (0) | 2024.02.19 |

